|
Some short thoughts
About
1a. "Entanglement" in quantum physics:
One of the mysteries that physicists don't understand within quantum mechanics is the observation that when e.g. two photons are emitted in different directions, they are always complementary in their direction of spin (clockwise - anti-clockwise), however far they are sent from each other.
Einstein, in a discussion with Bohr, meant that the photons must have been complementary from "start" like a right-hand glove and a lesft-hand glove. While Bohr believed in a kind of invisible connection. It's now regarded as proved through Bell's theorem and Aspect's experiments* that Bohr was right and there must be a so-called "entanglement" between the two photons. However, what says that not both were right? Especially from the views of the model (länk) here where complementarity is the fundamental principle behind the concept of dimensions?
How to interpret this entanglement - where any connection via something in light velocity is excluded?
- Could we interpret it as just a primary definition of d-degree 1 in our model, equivalent with Distance as physical concept and timeless?
- Another suggestion is to understand the entanglement in terms of a memory, a memory from underlying, deeper (~ higher) dimension degrees (d-degrees), like memories can connect us with people far away.
These two suggestions are naturally linked in our model, since 1 d-degree get debranched in each step from higher to lower d-degrees.
*Aspect's experiment implied measurements of the branched way of the two photons in perpendicular directions, thus was a 2-dimensional measurement.
If there were no coupling between the two outcomes, the maximum result of Bell’s formula should be +/- 2 (details and math here neglected), But the experiments did show on a maximum of +/- 2√2, the expected result of an entanglement
What could be the result in a 3-dimensionl measurement?
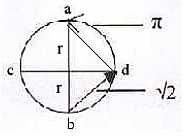 |
Assuming the definition of a dimension as characterized by two complementary “end-poles” (a-b, c-d in the figure), the shortest step between the poles b-a in an 1-dimensional world would be 2 r and the shortest step in a 2-dimensional world could be 2√2, b-d-a., i.e., via d-degree 2.
In a 3-dimensional world, the shortest way could perhaps be a circular one? |
Fig Q-1: A way to imagine Aspect's two results?
The entanglement should become an expression for what we have seen as the outer connection = the unpolarized lower d-degree 1 (b-a) in this example as the element of a structure, (no motion).
A note about the entanglement: Suppose we have a jelly roll, spiralled towards us and cut two equal slices of it, then lay them down, separating them outwards. The slices get opposite "spin", spiralled clockwise - anticlockwise.
This is just because division, the polarization, occurs from a center, the one between them, and the force is the direction "outwards", only defined as that through the relation to a center. (Couldn't it support the basic postulates in the model here?)
About
1b. The ENCODE Project: (http://www.genome.gov/10005107)
DNA in our cells includes a lot of parts that are not genes and don't code for proteins. In the ENCODE project thousands of scientists are trying to understand the role of these other parts. Much of what they find concerns the regulation of genes, which genes are transcribed when and such things through "transcription factors". There are small RNA strings too, which appear as intermediaries in the "3-dimensional" network.
A similarity with syntax or grammar of a language in relation to spoken words feels obvious.
One kind of operation is called "RNA-editing". A usual such editing seems to be the exchange of an A-nucleotide to a G-nucleotide, a process that goes via the common parent of both, Inosine (I).

Fig Q-2: RNA-editing A → G via Inosine
This RNA-editing resembles the guess about black holes (point 8 in file x1), an exchange via the common source, before a step of polarization.
(What's known about the function of this editing?)
___________________________
About
2. Impact of observations in quantum mechanical experiments?
It's often expressed in that way, that the very observation or measurement has an impact on the results of an experiment.
The wave functions of a photon don't allow for deciding a position of the quanta when emitted in a room, only for probabilities of where it may be. First an observation, a measurement, "get it" to exist as a "particle", or gives an answer Yes, here it is, or No, not here.
If this description is correct (?), maybe not), then the "impact" of observers on the outcome may be only that one certain direction is defined, to an eye or an instrument, through the very existence of these receptors, nothing else?
We could perhaps find a similarity with someone who talks in a room, creating sound waves. Only the ear of a listener can imply that the waves become particularized words - but cannot be said to have any impact on the distribution of waves as such in the room?
(However, about the photon: if e.g. 5 measurements are made in different positions in the room simultaneously, could more than one of them give a Yes answer?
Repeated measurements should give a pattern of probabilities.)
______________________________
About
3. Probabilities in quantum mechanics:
A quanta as a photon, regarded as a particle, should have a certain, identifiable position in a space at each moment. This is not allowed in quantum mechanics (Heisenberg's uncertainty principle). Through wave functions it's only possible to decide its position in terms of probabilities of its existence here or there.
This probability is the square of the amplitude of the wave.
Since amplitude is a distance from some zero-line, it's 1-dimensional. Thus, the square of it and hence a probability should be a 2-dimensional property.
When probabilities in physicists' calculations become = 1 or even >1 it seems to be regarded as wrong answers. Hence, the amplitudes of a wave should never be allowed to be 1, equal to its wavelength (?) or higher. (See a speculation in p.4 below.)
However, couldn't we suspect that a probability = 1 just becomes a truth - or more than true if with higher values, revealing a deeper, more comprehensive reality?
The "wrong" answer could be suspected to represent a step (a quantum jump) toward a higher d-degree, 2 to d-degree 3 (or even higher), where new rules prevail, with the wave functions now identified as non-linear ones with relevance limited to lower d-degree(s)?
How do jumps of electrons between orbitals in Bohr's atomic model get transformed to wave functions of emitted photons? Some momentary transition via a wave phase? In the Lyman-Balmer-Paschen-Brackett series for calculation of wave lengths of spectral lines from hydrogen, the inversion of wave lengths are given by intervals between inverted integers squared, from numbers 1, 2, 3, 4 to next higher integers (times a constant).
_________________________________
About
4. Particle - wave duality of light:
A very simple-minded speculation:
Are there possibly some internal changes like partial inversions when a wave transforms to a particularized quantum? Some special factor or factors changing in the wave functions as a condition for getting "strength" enough (packed enough) to serve as a particle?
In basic lectures of physics a sine wave is described as a projection outwards of a rotating vector in a unity circle:
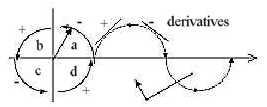
Fig.Q-3: Particle - wave
The projection implies that e.g. upper half of a turn of the rotating vector, from 0o to 180o, is mirrored, with derivatives changing signs in directions.
Simultaneously, if the sine wave shall transform back from wavy type to a circle (like a particle), there has to be a change in the phase of half a wavelength. In inward direction a reverse of the phase. It could resemble how a water wave, when meeting a hindrance, brakes and its kinetic energy of motion gets built in into the wavy structure...?
Cf. particles described by physicists as "motions in fields" - "of enough strength" (said about Higgs particle in TV).
_____________________________
About
5. Transformation of photons through steps in a dimension chain?
It's now and then said by physicists that a photon emitted from a source in an experiment may be overall in the room before it's finally get detected somewhere (as waves or quanta). Suppose it is, really overall.
With our model (länk) in mind, we could test to think of the photon's "phases" of existence as a chain of d-degree steps:
a) The very emission from the source as a center seen in terms of divergence, direction outwards from a 0-pole, d-degree 4 to 4b.
b) The room filled with the photon as a transformation to its 3-dimensional existence (possible to interpret perhaps in terms of an invisible substance), where one pole geometrically remains radial in the primary, geometrical definitions of our model.
c) Meeting a plane screen with slits transformed to a 2-dimensional surface wave.
d) Linear, 1-dimensional pathways of the wave getting more or less selected by the slits (?), simultaneously as d-degree 1, which in our model has the outer poles 2a - 2 (~ max - min of waves).
e) The last step 1 to 0 (the photon as a point) has the "outer poles" 1a - 1b. Hence, the polarization into complementary light - dark stripes will appear - as an endogenous property. (?)
____________________________________________________
|


